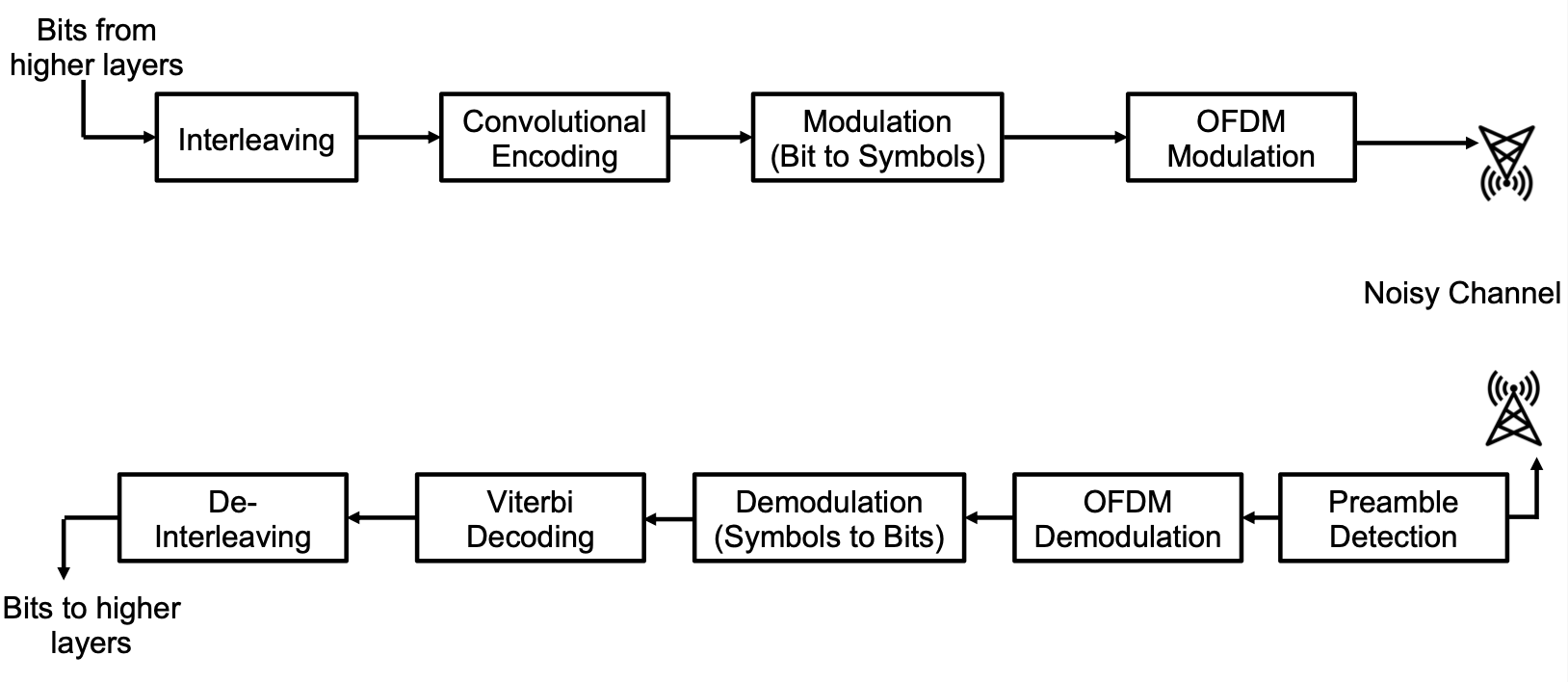
Physical layer is the lowest layer in the OSI model. In this project, I explored a simplified Wi- Fi physical layer model on how our bits are manipulated and transmitted. Meanwhile, a Wi-Fi receiver that could receive the message generated by a simulated Wi-Fi transmitter is implemented.

Figure 1. Flow chart of WifiReceiver
For Viterbi Decoder, I choose the soft decoding approach, because it is more robust than hard decoding. The trellis that is used in our 4QAM modulation is shown below.
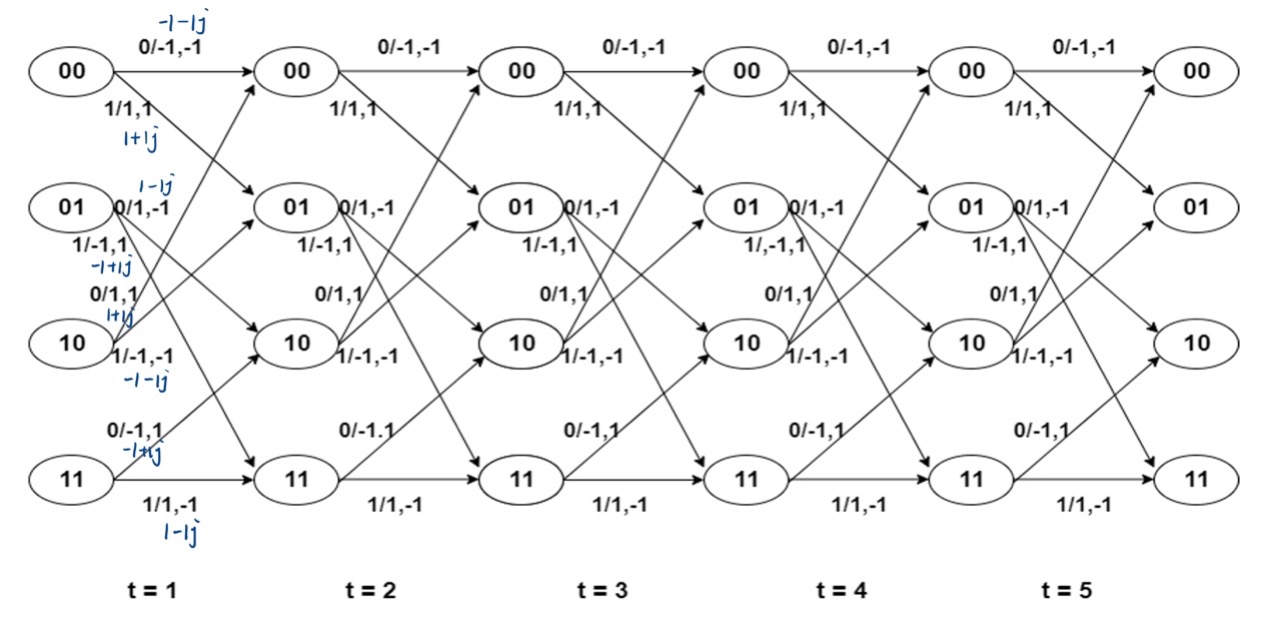
Figure 2. Trellis - 4QAM
In my code, two functions: my_v_decode() and viterbi_step_soft() is used to perform this decoding. viterbi_step_soft() accepts a signal point (complex number) and the shortest paths (and their costs) as input. It performs the calculation for this certain layer and returns the shortest paths and costs for the next layer. my_v_decode() accepts series of signal points and call viterbi_step_soft() for each signal point. At last, it identifies the shortest path and converts it to the bits we want. Note that I used a greedy algorithm on the calculation of the shortest path. For each state in the same layer, only the path with minimum cost will be stored. This algorithm keeps this decoding process simple.
Length inference is another difficulty in this assignment. In the beginning, the message length information in the bitstream, which is packed before message bits in layer 1, is used to truncate the final message. However, in my later experiment, I found these bits are not reliable since they are not convolutional encoded by the transmitter. The hard decoding approach to restoring these bits performs poorly when SNR is too low. In the end, I use the occurrence of value 0 in my final decoded message to determine the end of our message. Because we only have textual input (i.e., any sequence of ASCII characters), we will not use the NULL character in our normal messages. Meanwhile, in the WifiTransmitter, the input message is padded with zeros to ensure its length is a multiple of nfft. This characteristic helps me to detect message length more accurately. However, this message length detection algorithm could fail when the bits in our transmitted message happen to be exactly a multiple of nfft. To fix this issue, I have an idea of combining these two methods and switching between them using our estimated noise level for each signal we received. Also, a more straightforward way is convolutional encoding the length bits with our message.
To improve the receiver’s performance under poor SNR conditions, two designs were applied. The first one is the length inference method mentioned above. The second one is preamble detection. In level 4, we have a noisy signal before and after our message. The key challenge is how to locate our preamble. In my implementation, the correlation between the noisy and noise-free preamble signal is calculated. By selecting the position that has the maximum correlation value, the preamble signal can be located easily. In more than half of the cases, my implementation could decode short messages (e.g., hello world) where SNR equals -3.